Quiz: Binary Search Trees
Show that if a node in a binary search tree has two children, then its successor Y has no left child and its predecessor has no right child. (The proofs are symmetric. Hints: Rule out where the successor cannot be to narrow down to where it must be. Draw Pictures!!!)
a. Prove by contradiction that the successor Y cannot be an ancestor of X, so Y must be in a subtree.
b. Identify and prove the subtree of X that successor Y must be in.
c. Show by contradiction that successor Y cannot have a left child.
d. Indicate how this proof would be changed for predecessor.
Delete the nodes with keys 10 and 27 from this Binary Search Tree, indicating for each case what “if/elseif” block is executed. (You will need to apply the cases carefully to get this right: refer to the text or web notes. “Eyeballing” it may lead to a legal tree that would not result from the code.)
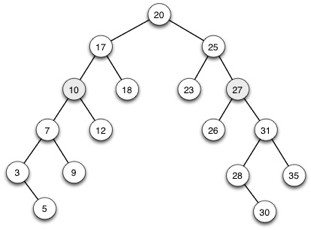
a. Lines executed in deletion of 10:
b. Lines executed in deletion of 27:
